Experimental Probability
The chance or occurrence of a particular event is termed its probability. The value of a probability lies between 0 and 1 which means if it is an impossible event, the probability is 0 and if it is a certain event, the probability is 1. The probability that is determined on the basis of the results of an experiment is known as experimental probability. This is also known as empirical probability.

What is Experimental Probability?
Experimental probability is a probability that is determined on the basis of a series of experiments. A random experiment is done and is repeated many times to determine their likelihood and each repetition is known as a trial. The experiment is conducted to find the chance of an event to occur or not to occur. It can be tossing a coin, rolling a die, or rotating a spinner. In mathematical terms, the probability of an event is equal to the number of times an event occurred ÷ the total number of trials. For instance, you flip a coin 30 times and record whether you get a head or a tail. The experimental probability of obtaining a head is calculated as a fraction of the number of recorded heads and the total number of tosses. P(head) = Number of heads recorded ÷ 30 tosses.
Experimental Probability Formula
The experimental probability of an event is based on the number of times the event has occurred during the experiment and the total number of times the experiment was conducted. Each possible outcome is uncertain and the set of all the possible outcomes is called the sample space. The formula to calculate the experimental probability is: P(E) = Number of times an event occurs/Total number of times the experiment is conducted
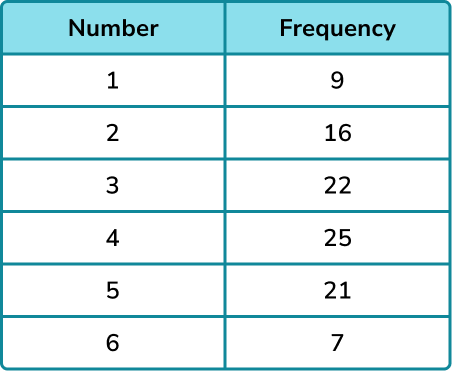
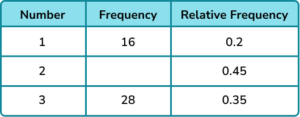
Consider an experiment of rotating a spinner 50 times. The table given below shows the results of the experiment conducted. Let us find the experimental probability of spinning the color - blue.
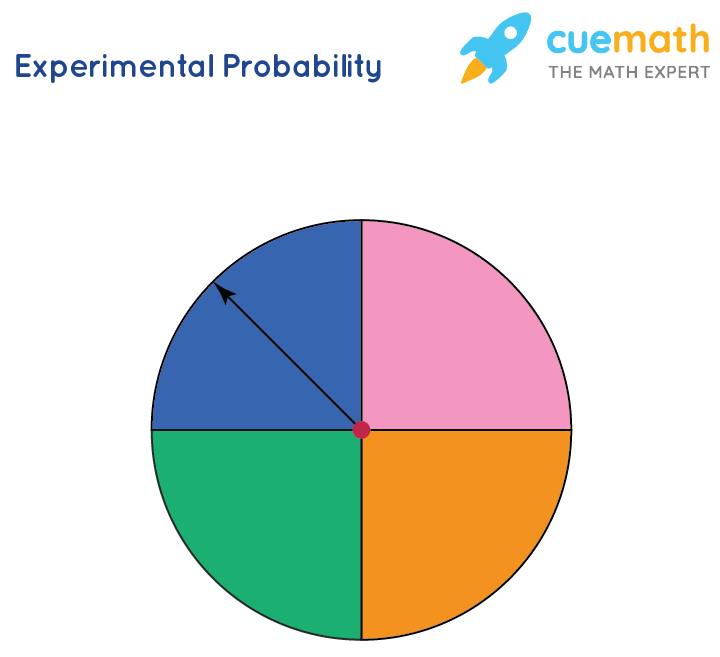
The experimental probability of spinning the color blue = 10/50 = 1/5 = 0.2 = 20%
Experimental Probability vs Theoretical Probability
Experimental results are unpredictable and may not necessarily match the theoretical results. The results of experimental probability are close to theoretical only if the number of trials is more in number. Let us see the difference between experimental probability and theoretical probability.
Experimental Probability Examples
Here are a few examples from real-life scenarios.
a) The number of cookies made by Patrick per day in this week is given as 4, 7, 6, 9, 5, 9, 5.
Based on this data, what is the reasonable estimate of the probability that Patrick makes less than 6 cookies the next day?
P(< 6 cookies) = 3/7 = 0.428 = 42%
b) Find the reasonable estimate of the probability that while ordering a pizza, the next order will not be of a pepperoni topping.
Based on this data , the reasonable estimate of the probability that the next type of toppings that would get ordered is not a pepperoni will be 15/20 = 3/4 = 75%
Related Sections
- Card Probability
- Conditional Probability Calculator
- Binomial Probability Calculator
- Probability Rules
- Probability and Statistics
Important Notes
- The sum of the experimental probabilities of all the outcomes is 1.
- The probability of an event lies between 0 and 1, where 0 is an impossible event and 1 denotes a certain event.
- Probability can also be expressed in percentage.
Examples on Experimental Probability
Example 1: The following table shows the recording of the outcomes on throwing a 6-sided die 100 times.
Find the experimental probability of: a) Rolling a four; b) Rolling a number less than four; c) Rolling a 2 or 5
Experimental probability is calculated by the formula: Number of times an event occurs/Total number of trials
a) Rolling a 4: 17/100 = 0.17
b) Rolling a number less than 4: 56/100 = 0.56
c) Rolling a 2 or 5: 31/100 = 0.31
Example 2: The following set of data shows the number of messages that Mike received recently from 6 of his friends. 4, 3, 2, 1, 6, 8. Based on this, find the probability that Mike will receive less than 2 messages next time.
Mike has received less than 2 messages from 2 of his friends out of 6.
Therefore, P(<2) = 2/6 = 1/3
go to slide go to slide

Book a Free Trial Class
Practice Questions on Experimental Probability
Frequently asked questions (faqs), how do you find the experimental probability.
The experimental probability of an event is based on actual experiments and the recordings of the events. It is equal to the number of times an event occurred divided by the total number of trials.
What is the Experimental Probability of rolling a 6?
The experimental probability of rolling a 6 is 1/6. A die has 6 faces numbered from 1 to 6. Rolling the die to get any number from 1 to 6 is the same and the probability (of getting a 6) = Number of favorable outcomes/ total possible outcomes = 1/6.
What is the Difference Between Theoretical and Experimental Probability?
Theoretical probability is what is expected to happen and experimental probability is what has actually happened in the experiment.
Do You Simplify Experimental Probability?
Yes, after finding the ratio of the number of times the event occurred to the total number of trials conducted, the fraction which is obtained is simplified.
Which Probability is More Accurate, Theoretical Probability or Experimental Probability?
Theoretical probability is more accurate than experimental probability. The results of experimental probability are close to theoretical only if the number of trials are more in number.

Experimental Probability
Experimental probability: introduction, experimental probability: definition, experimental probability formula, solved examples, practice problems, frequently asked questions.
In mathematics, probability refers to the chance of occurrence of a specific event. Probability can be measured on a scale from 0 to 1. The probability is 0 for an impossible event. The probability is 1 if the occurrence of the event is certain.
There are two approaches to study probability: experimental and theoretical.
Suppose you and your friend toss a coin to decide who gets the first turn to ride a new bicycle. You choose “heads” and your friend chooses “tails.”

Can you guess who will win? No! You have $\frac{1}{2}$ a chance of winning and so does your friend. This is theoretical since you are predicting the outcome based on what is expected to happen and not on the basis of outcomes of an experiment.
So, what is the experimental probability? Experimental probability is calculated by repeating an experiment and observing the outcomes. Let’s understand this a little better.
Recommended Games

Experimental probability, or empirical probability, is the probability calculated by performing actual experiments and gathering or recording the necessary information. How would you define an experiment? The math definition of an experiment is “a process or procedure that can be repeated and that has a set of well-defined possible results or outcomes.”

Consider the same example. Suppose you flip the coin 50 times to see whether you get heads or tails, and you record the outcomes. Suppose you get heads 20 times and tails 30 times. Then the probability calculated using these outcomes is experimental probability. Here, t he experimental meaning is connected with such experiments used to determine the probability of an event.
Now that you know the meaning of experimental probability, let’s understand its formula.
Experimental Probability for an Event A can be calculated as follows:
P(E) $= \frac{Number of occurance of the event A}{Total number of trials}$
Let’s understand this with the help of the last example.

A coin is flipped a total of 50 times. Heads appeared 20 times. Now, what is the experimental probability of getting heads?
E xperimental probability of getting heads $= \frac{Number of occurrences}{Total number of trials}$
P (Heads) $= \frac{20}{50} = \frac{2}{5}$
P (Tails) $= \frac{30}{50} = \frac{3}{5}$
Experimental Probability vs. Theoretical Probability
Theoretical probability expresses what is expected. On the other hand, experimental probability explains how frequently an event occurred in an experiment.
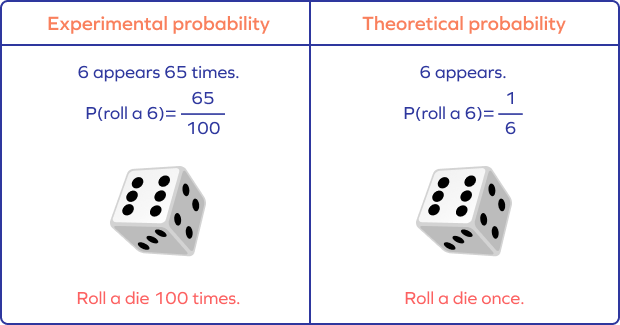
If you roll a die, the theoretical probability of getting any particular number, say 3, is $\frac{1}{6}$.
However, if you roll the die 100 times and record how many times 3 appears on top, say 65 times, then the experimental probability of getting 3 is $\frac{65}{100}$.
Theoretical probability for Event A can be calculated as follows:
P(A) $= \frac{Number of outcomes favorable to Event A}{Number of possible outcomes}$
In the example of flipping a coin, the theoretical probability of the occurrence of heads (or tails) on tossing a coin is
P(H) $= \frac{1}{2}$ and P(T) $= \frac{1}{2}$ (since possible outcomes are $2 -$ head or tail)
Experimental Probability: Examples
Let’s take a look at some of the examples of experimental probability .
Example 1: Ben tried to toss a ping-pong ball in a cup using 10 trials, out of which he succeeded 4 times.

P(win) $= \frac{Number of success}{Number of trials}$
$= \frac{4}{10}$
$= \frac{2}{5}$
Example 2: Two students are playing a game of die. They want to know how many times they land on 2 on the dice if the die is rolled 20 times in a row.

The experimental probability of rolling a 2
$= \frac{Number of times 2 appeared}{Number of trials}$
$= \frac{5}{20}$
$= \frac{1}{4}$
1. Probability of an event always lies between 0 and 1.
2. You can also express the probability as a decimal and a percentage.
Experimental probability is a probability that is determined by the results of a series of experiments. Learn more such interesting concepts at SplashLearn .
1. Leo tosses a coin 25 times and observes that the “head” appears 10 times. What is the experimental probability of getting a head?
P(Head) $= \frac{Number of times heads appeared}{Total number of trials}$
$= \frac{10}{25}$
$= \frac{2}{5}$
$= 0.4$
2. The number of cakes a baker makes per day in a week is given as 7, 8, 6, 10, 2, 8, 3. What is the probability that the baker makes less than 6 cakes the next day?
Solution:
Number of cakes baked each day in a week $= 7, 8, 6, 10, 2, 8, 3$
Out of 7 days, there were 2 days (highlighted in bold) on which the baker made less than 6 cookies.
P$(< 6 $cookies$) = \frac{2}{7}$
3. The chart below shows the number of times a number was shown on the face of a tossed die. What was the probability of getting a 3 in this experiment?

Number of times 3 showed $= 7$
Number of tosses $= 30$
P(3) $= \frac{7}{30}$
4. John kicked a ball 20 times. He kicked 16 field goals and missed 4 times . What is the experimental probability that John will kick a field goal during the game?
Solution:
John succeeded in kicking 16 field goals. He attempted to kick a field goal 20 times.
So, the number of trials $= 20$
John’s experimental probability of kicking a field goal $= \frac{Successful outcomes} {Trials attempted} = \frac{16}{20}$
$= \frac{4}{5}$
$= 0.8$ or $80%$
5. James recorded the color of bikes crossing his street. Of the 500 bikes, 10 were custom colors, 100 were white, 50 were red, 120 were black, 100 were silver, 60 were blue, and 60 were gray. What is the probability that the car crossing his street is white?
Number of white bikes $= 100$
Total number of bikes $= 500$
P(white bike) $= \frac{100}{500} = \frac{1}{5}$
Attend this quiz & Test your knowledge.
In a class, a student is chosen randomly in five trials to participate in 5 different events. Out of chosen students, 3 were girls and 2 were boys. What is the experimental probability of choosing a boy in the next event?
A manufacturer makes 1000 tablets every month. after inspecting 100 tablets, the manufacturer found that 30 tablets were defective. what is the probability that you will buy a defective tablet, the 3 coins are tossed 1000 times simultaneously and we get three tails $= 160$, two tails $= 260$, one tail $= 320$, no tails $= 260$. what is the probability of occurrence of two tails, the table below shows the colors of shirts sold in a clothing store on a particular day and their respective frequencies. use the table to answer the questions that follow. what is the probability of selling a blue shirt.

Jason leaves for work at the same time each day. Over a period of 327 working days, on his way to work, he had to wait for a train at the railway crossing for 68 days. What is the experimental probability that Jason has to wait for a train on his way to work?
What is the importance of experimental probability?
Experimental probability is widely used in research and experiments in various fields, such as medicine, social sciences, investing, and weather forecasting.
Is experimental probability always accurate?
Predictions based on experimental probability are less reliable than those based on theoretical probability.
Can experimental probability change every time the experiment is performed?
Since the experimental probability is based on the actual results of an experiment, it can change when the results of an experiment change.
What is theoretical probability?
The theoretical probability is calculated by finding the ratio of the number of favorable outcomes to the total number of probable outcomes.
RELATED POSTS
- Length Conversion – Metric and Customary System, Examples
- How Many Weeks Are There in a Month? Definition with Examples
- Analog Clock – Definition, Clock Face, Clock Hands, Examples, Facts
- Slope of Parallel Line: Formula, Derivation, Example
- Milliliter – Definition with Examples

Math & ELA | PreK To Grade 5
Kids see fun., you see real learning outcomes..
Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.
Parents, Try for Free Teachers, Use for Free

- Mathematicians
- Math Lessons
- Square Roots
- Math Calculators
- Experimental Probability – Explanation & Examples
JUMP TO TOPIC
What is experimental probability?
Practice questions, experimental probability – explanation & examples.

Experimental probability is the probability determined based on the results from performing the particular experiment.
In this lesson we will go through:
- The meaning of experimental probability
- How to find experimental probability

The ratio of the number of outcomes favorable to an event to the total number of trials of the experiment.
Experimental Probability can be expressed mathematically as:
$P(\text{E}) = \frac{\text{number of outcomes favorable to an event}}{\text{total number of trials of the experiment}}$
Let’s go back to the die tossing example. If after 12 throws you get one 6, then the experimental probability is $\frac{1}{12}$. You can compare that to the theoretical probability. The theoretical probability of getting a 6 is $\frac{1}{6}$. This means that in 12 throws we would have expected to get 6 twice.
Similarly, if in those 12 tosses you got a 1 five times, the experimental probability is $\frac{5}{12}$.

How do we find experimental probability?
Now that we understand what is meant by experimental probability, let’s go through how it is found.
To find the experimental probability of an event, divide the number of observed outcomes favorable to the event by the total number of trials of the experiment.
Let’s go through some examples.
Example 1: There are 20 students in a class. Each student simultaneously flipped one coin. 12 students got a Head. From this experiment, what was the experimental probability of getting a head?
Number of coins showing Heads: 12
Total number of coins flipped: 20
$P(\text{Head}) = \frac{12}{20} = \frac{3}{5}$
Example 2: The tally chart below shows the number of times a number was shown on the face of a tossed die.
a. What was the probability of a 3 in this experiment?
b. What was the probability of a prime number?
First, sum the numbers in the frequency column to see that the experiment was performed 30 times. Then find the probabilities of the specified events.
a. Number of times 3 showed = 7
Number of tosses = 30
$P(\text{3}) = \frac{7}{30}$
b. Frequency of primes = 6 + 7 + 2 = 15
Number of trials = 30
$P(\text{prime}) = \frac{15}{30} = \frac{1}{2}$
Experimental probability can be used to predict the outcomes of experiments. This is shown in the following examples.
Example 3: The table shows the attendance schedule of an employee for the month of May.
a. What is the probability that the employee is absent?
b. How many times would we expect the employee to be present in June?
a. The employee was absent three times and the number of days in this experiment was 31. Therefore:
$P(\text{Absent}) = \frac{3}{31}$
b. We expect the employee to be absent
$\frac{3}{31} × 30 = 2.9 ≈ 3$ days in June
Example 4: Tommy observed the color of cars owned by people in his small hometown. Of the 500 cars in town, 10 were custom colors, 100 were white, 50 were red, 120 were black, 100 were silver, 60 were blue, and 60 were grey.
a. What is the probability that a car is red?
b. If a new car is bought by someone in town, what color do you think it would be? Explain.
a. Number of red cars = 50
Total number of cars = 500
$P(\text{red car}) = \frac{50}{500} = \frac{1}{10}$
b. Based on the information provided, it is most likely that the new car will be black. This is because it has the highest frequency and the highest experimental probability.
Now it is time for you to try these examples.
The table below shows the colors of jeans in a clothing store and their respective frequencies. Use the table to answer the questions that follow.
- What is the probability of selecting a brown jeans?
- What is the probability of selecting a blue or a white jeans?
On a given day, a fast food restaurant notices that it sold 110 beef burgers, 60 chicken sandwiches, and 30 turkey sandwiches. From this observation, what is the experimental probability that a customer buys a beef burger?
Over a span of 20 seasons, a talent competition notices the following. Singers won 12 seasons, dancers won 2 seasons, comedians won 3 seasons, a poet won 1 season, and daring acts won the other 2 seasons.
a. What is the experimental probability of a comedian winning a season?
b. From the next 10 seasons, how many winners do you expect to be dancers?
Try this at home! Flip a coin 10 times. Record the number of tails you get. What is your P(tail)?
Number of brown jeans = 25
Total Number of jeans = 125
$P(\text{brown}) = \frac{25}{125} = \frac{1}{5}$
Number of jeans that are blue or white = 75 + 20 = 95
$P(\text{blue or white}) = \frac{95}{125} = \frac{19}{25}$
Number of beef burgers = 110
Number of burgers (or sandwiches) sold = 200
$P(\text{beef burger}) = \frac{110}{200} = \frac{11}{20}$
a. Number of comedian winners = 3
Number of seasons = 20
$P(\text{comedian}) = \frac{3}{20}$
b. First find the experimental probability that the winner is a dancer.
Number of winners that are dancers = 2
$P(\text{dancer}) = \frac{2}{20} = \frac{1}{10}$
Therefore we expect
$\frac{1}{10} × 10 = 1$ winner to be a dancer in the next 10 seasons.
To find your P(tail) in 10 trials, complete the following with the number of tails you got.
$P(\text{tail}) = \frac{\text{number of tails}}{10}$
Previous Lesson | Main Page | Next Lesson
- Maths Notes Class 9
- NCERT Solutions Class 9
- RD Sharma Solutions Class 9
- Maths Formulas Class 9
- Class 9 Syllabus
- Class 9 Revision Notes
- Physics Notes Class 9
- Chemistry Notes Class 9
- Biology Notes Class 9
- History Notes class 9
- Geography Notes class 9
- Social science Notes class 9
- Experimental Probability
Experimental probability , also known as empirical probability , is a concept in mathematics that deals with estimating the likelihood of an event occurring based on actual experimental results. Unlike theoretical probability , which predicts outcomes based on known possibilities, experimental probability is derived from real-life experiments and observations.
To understand this better, imagine flipping a coin. The theoretical probability of landing heads is 50% or 1/2. However, if you actually flip the coin 100 times and record the outcomes, you might get heads 48 times. The experimental probability of getting heads would then be 48/100 or 0.48.
In this article, we will explore the concept of experimental probability, its significance, and how it differs from theoretical probability. We will discuss the formula for calculating experimental probability, provide examples to illustrate its application.
Table of Content
What is Probability?
What is experimental probability, formula for experimental probability, examples of experimental probability, what is theoretical probability, experimental probability vs theoretical probability.
- Solved Examples
- Practice Problems
The branch of mathematics that tells us about the likelihood of the occurrence of any event is the probability . Probability tells us about the chances of happening an event.
The probability of any element that is sure to occur is One(1) whereas the probability of any impossible event is Zero(0). The probability of all the elements ranges between 0 to 1.
There are two ways of studying probability that are
- Theoretical Probability
Now let’s learn about both in detail.
Experimental probability is a type of probability that is calculated by conducting an actual experiment or by performing a series of trials to observe the occurrence of an event. It is also known as empirical probability.
To calculate experimental probability, you need to conduct an experiment by repeating the event multiple times and observing the outcomes. Then, you can find the probability of the event occurring by dividing the number of times the event occurred by the total number of trials.

The experimental Probability for Event A can be calculated as follows:
P(E) = (Number of times an event occur in an experiment) / (Total number of Trials)
Now, as we learn the formula, let’s put this formula in our coin-tossing case. If we tossed a coin 10 times and recorded a head 4 times and a tail 6 times then the Probability of Occurrence of Head on tossing a coin:
P(H) = 4/10
Similarly, the Probability of Occurrence of Tails on tossing a coin:
P(T) = 6/10
Theoretical Probability deals with assumptions in order to avoid unfeasible or expensive repetition experiments. The theoretical Probability for an Event A can be calculated as follows:
P(A) = Number of outcomes favorable to Event A / Number of all possible outcomes
Now, as we learn the formula, let’s put this formula in our coin-tossing case. In tossing a coin, there are two outcomes: Head or Tail.
Hence, The Probability of occurrence of Head on tossing a coin is
Similarly, The Probability of the occurrence of a Tail on tossing a coin is

There are some key differences between Experimental and Theoretical Probability , some of which are as follows:
- Probability in Maths
- Probability Distribution
- Bayes’ Theorem
Solved Examples of Experimental Probability
Example 1. Let’s take an example of tossing a coin, tossing it 40 times , and recording the observations. By using the formula, we can find the experimental probability for heads and tails as shown in the below table.
Number of Trail Outcome Number of Trail Outcome Number of Trail Outcome Number of Trail Outcome First H Eleventh T Twenty-first T Thirty-first T Second T Twelfth T Twenty-second H Thirty-second H Third T Thirteenth H Twenty-third T Thirty-third T Fourth H Fourteenth H Twenty-fourth H Thirty-fourth H Fifth H Fifteenth H Twenty-fifth T Thirty-fifth T Sixth H Sixteenth H Twenty-sixth H Thirty-sixth T Seventh T Seventeenth T Twenty-seventh T Thirty-seventh T Eighth H Eighteenth T Twenty-eighth T Thirty-eighth H Ninth T Nineteenth T Twenty-ninth T Thirty-ninth T Tenth H Twentieth T Thirtieth H Fortieth T The formula for experimental probability: P(H) = Number of Heads ÷ Total Number of Trials = 16 ÷ 40 = 0.4 Similarly, P(H) = Number of Tails ÷ Total Number of Trials = 24 ÷ 40 = 0.6 P(H) + P(T) = 0.6 + 0.4 = 1 Note: Repeat this experiment for ‘n’ times and then you will find that the number of times increases, the fraction of experimental probability comes closer to 0.5. Thus if we add P(H) and P(T), we will get 0.6 + 0.4 = 1 which means P(H) and P(T) is the only possible outcomes.
Example 2. A manufacturer makes 50,000 cell phones every month. After inspecting 1000 phones, the manufacturer found that 30 phones are defective. What is the probability that you will buy a phone that is defective? Predict how many phones will be defective next month.
Experimental Probability = 30/1000 = 0.03 0.03 = (3/100) × 100 = 3% The probability that you will buy a defective phone is 3% ⇒ Number of defective phones next month = 3% × 50000 ⇒ Number of defective phones next month = 0.03 × 50000 ⇒ Number of defective phones next month = 1500
Example 3. There are about 320 million people living in the USA. Pretend that a survey of 1 million people revealed that 300,000 people think that all cars should be electric. What is the probability that someone chosen randomly does not like the electric car? How many people like electric cars?
Now the number of people who do not like electric cars is 1000000 – 300000 = 700000 Experimental Probability = 700000/1000000 = 0.7 And, 0.7 = (7/10) × 100 = 70% The probability that someone chose randomly does not like the electric car is 70% The probability that someone like electric cars is 300000/1000000 = 0.3 Let x be the number of people who love electric cars ⇒ x = 0.3 × 320 million ⇒ x = 96 million The number of people who love electric cars is 96 million.
Practice Problems on Experimental Probability
Problem 1: A coin is flipped 200 times, and it lands on heads 120 times. What is the experimental probability of getting heads?
Problem 2: A die is rolled 50 times, and the number 3 appears 8 times. What is the experimental probability of rolling a 3?
Problem 3: In a class survey, 150 students were asked if they prefer reading books or watching movies. 90 students said they prefer watching movies. What is the experimental probability that a randomly chosen student prefers watching movies?
Problem 4: A bag contains 5 red, 7 blue, and 8 green marbles. If 40 marbles are drawn at random with replacement, and 12 of them are red, what is the experimental probability of drawing a red marble?
Problem 5: A basketball player made 45 successful free throws out of 60 attempts. What is the experimental probability that the player will make a free throw?
Problem 6: During a game, a spinner is spun 80 times, landing on a specific section 20 times. What is the experimental probability of the spinner landing on that section?
FAQs on Experimental Probability
Define experimental probability..
Probability of an event based on an actual trail in physical world is called experimental probability.
How is Experimental Probability calculated?
Experimental Probability is calculated using the following formula: P(E) = (Number of trials taken in which event A happened) / Total number of trials
Can Experimental Probability be used to predict future outcomes?
No, experimental probability can’t be used to predict future outcomes as it only achives the theorectical value when the trails becomes infinity.
How is Experimental Probability different from Theoretical Probability?
Theoretical probability is the probability of an event based on mathematical calculations and assumptions, whereas experimental probability is based on actual experiments or trials.
What are some Limitations of Experimental Probability?
There are some limitation of experimental probability, which are as follows: Experimental probability can be influenced by various factors, such as the sample size, the selection process, and the conditions of the experiment. The number of trials conducted may not be sufficient to establish a reliable pattern, and the results may be subject to random variation. Experimental probability is also limited to the specific conditions of the experiment and may not be applicable in other contexts.
Can Experimental Probability of an event be a negative number if not why?
As experimental probability is given by: P(E) = Number of trials taken in which event A happened/Total number of trials Thus, it can’t be negative as both number are count of something and counting numbers are 1, 2, 3, 4, …. and they are never negative.
What are Types of Probability?
There are two forms of calculating the probability of an event that are, Theoretical Probability Experimental Probability
Similar Reads
- CBSE Class 10 Maths Notes PDF: Chapter Wise Notes 2024 Math is an important subject in CBSE Class 10th Board exam. So students are advised to prepare accordingly to score well in Mathematics. Mathematics sometimes seems complex but at the same time, It is easy to score well in Math. So, We have curated the complete CBSE Class 10 Math Notes for you to pr 15+ min read
Chapter 1: Real Numbers
- Real Numbers Real Numbers are continuous quantities that can represent a distance along a line, as Real numbers include both rational and irrational numbers. Rational numbers occupy the points at some finite distance and irrational numbers fill the gap between them, making them together to complete the real line 10 min read
- Euclid Division Lemma Euclid's Division Lemma which is one of the fundamental theorems proposed by the ancient Greek mathematician Euclid which was used to prove various properties of integers. The Euclid's Division Lemma also serves as a base for Euclid's Division Algorithm which is used to find the GCD of any two numbe 5 min read
- Fundamental Theorem of Arithmetic The Fundamental Theorem of Arithmetic is a useful method to understand the prime factorization of any number. The factorization of any composite number can be uniquely written as a multiplication of prime numbers, regardless of the order in which the prime factors appear. The figures above represent 7 min read
- HCF / GCD and LCM - Definition, Formula, Full Form, Examples The Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), and Lowest Common Multiple (LCM) are fundamental concepts in mathematics, especially in number theory and arithmetic. The full form of HCF is the Highest Common Factor while the full form of LCM is the Least Common Mul 11 min read
- Irrational Numbers- Definition, Examples, Symbol, Properties Irrational numbers are real numbers that cannot be expressed as fractions. Irrational Numbers can not be expressed in the form of p/q, where p and q are integers and q ≠ 0. They are non-recurring, non-terminating, and non-repeating decimals. Irrational numbers are real numbers but are different from 12 min read
- Decimal Expansions of Rational Numbers Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, also. So in this article let's discuss some rational and irrational numbers an 6 min read
- Rational Numbers Rational numbers are a fundamental concept in mathematics, defined as numbers that can be expressed as the ratio of two integers, where the denominator is not zero. Represented in the form p/q (with p and q being integers), rational numbers include fractions, whole numbers, and terminating or repea 15+ min read
Chapter 2: Polynomials
- Algebraic Expressions in Math: Definition, Example and Equation An Algebraic Expression is a mathematical expression that is made of numbers, and variables connected with any arithmetical operation between them. Algebraic forms are used to define unknown conditions in real life or situations that include unknown variables. Algebraic expressions are a very import 14 min read
- Polynomial Formula Polynomial Formula gives the standard form of polynomial expressions. It specifies the arrangement of algebraic expressions according to their increasing or decreasing power of variables. Let's learn about various polynomial formulas and identities in detail. Table of Content What is Polynomial?Type 6 min read
- Types of Polynomials (Based on Terms and Degrees) Types of Polynomials: In mathematics, an algebraic expression is an expression built up from integer constants, variables, and algebraic operations. There are mainly four types of polynomials based on degree-constant polynomial (zero degree), linear polynomial ( 1st degree), quadratic polynomial (2n 9 min read
- Zeros of Polynomial Zeros of a Polynomial are those real, imaginary, or complex values when put in the polynomial instead of a variable, the result becomes zero (as the name suggests zero as well). Polynomials are used to model some physical phenomena happening in real life, they are very useful in describing situation 14 min read
- Geometrical meaning of the Zeroes of a Polynomial An algebraic identity is an equality that holds for any value of its variables. They are generally used in the factorization of polynomials or simplification of algebraic calculations. A polynomial is just a bunch of algebraic terms added together, for example, p(x) = 4x + 1 is a degree-1 polynomial 8 min read
- Factorization of Polynomial Factorization is the process in which we can find factors of either a given number or the algebraic expression using various techniques such as prime factorization, factorization using algebraic identities, and factorization of a quadratic polynomial using the middle term splitting method. Factoriza 12 min read
- Division Algorithm for Polynomials Polynomials are those algebraic expressions that contain variables, coefficients, and constants. For Instance, in the polynomial 8x2 + 3z - 7, in this polynomial, 8,3 are the coefficients, x and z are the variables, and 7 is the constant. Just as simple Mathematical operations are applied on numbers 5 min read
- Algebraic Identities Algebraic Identities are fundamental equations in algebra where the left-hand side of the equation is always equal to the right-hand side, regardless of the values of the variables involved. These identities play a crucial role in simplifying algebraic computations and are essential for solving vari 14 min read
- Relationship between Zeroes and Coefficients of a Polynomial Polynomials are algebraic expressions with constants and variables that can be linear i.e. the highest power o the variable is one, quadratic and others. The zeros of the polynomials are the values of the variable (say x) that on substituting in the polynomial give the answer as zero. While the coef 9 min read
- Division Algorithm Problems and Solutions Polynomials are made up of algebraic expressions with different degrees. Degree-one polynomials are called linear polynomials, degree-two are called quadratic and degree-three are called cubic polynomials. Zeros of these polynomials are the points where these polynomials become zero. Sometimes it ha 6 min read
Chapter 3: Pair of Linear equations in two variables
- Linear Equation in Two Variables Linear Equation in Two Variables: A Linear equation is defined as an equation with the maximum degree of one only, for example, ax = b can be referred to as a linear equation, and when a Linear equation in two variables comes into the picture, it means that the entire equation has 2 variables presen 9 min read
- Pair of Linear Equations in Two Variables Linear Equation in two variables are equations with only two variables and the exponent of the variable is 1. This system of equations can have a unique solution, no solution, or an infinite solution according to the given initial condition. Linear equations are used to describe a relationship betwe 11 min read
- Graphical Methods of Solving Pair of Linear Equations in Two Variables A system of linear equations is just a pair of two lines that may or may not intersect. The graph of a linear equation is a line. There are various methods that can be used to solve two linear equations, for example, Substitution Method, Elimination Method, etc. An easy-to-understand and beginner-fr 8 min read
- Solve the Linear Equation using Substitution Method Solving Linear Equation using the Substitution Method: The equation in which the highest power of the variable is always 1 is called a linear equation (or) the first-order equation. A linear equation's graph will always be a straight line. When the equation has only one variable and the highest degr 12 min read
- Solving Linear Equations Using the Elimination Method If an equation is written in the form ax + by + c = 0, where a, b, and c are real integers and the coefficients of x and y, i.e. a and b, are not equal to zero, it is said to be a linear equation in two variables. For example, 3x + y = 4 is a linear equation in two variables- x and y. The numbers th 10 min read
Chapter 4: Quadratic Equations
- Quadratic Equations Quadratic equation is a fundamental concept of algebra and mathematics, It is a second-degree equation that can be represented as ax2 + bx + c = 0. In this equation, x is an unknown variable, a, b, and c are constants, and a is not equal to 0. A quadratic Equation can be solved by using methods such 15+ min read
- Roots of Quadratic Equation Roots of Quadratic Equations are the values of the variable for which the quadratic equation gets satisfied. The roots of a quadratic equation are also called zeros of a quadratic equation. A quadratic equation is an equation in which the maximum power of a variable is 2. Hence, there can be a maxim 13 min read
- Solving Quadratic Equations Solving quadratic equations is a fundamental skill in mathematics that plays a crucial role in various fields such as physics, engineering, and finance. As Quadratic Equations occur almost everywhere in our real life. For example, even the problem of designing a playground can be formulated as a qua 9 min read
- How to find the Discriminant of a Quadratic Equation? Algebra can be defined as the branch of mathematics that deals with the study, alteration, and analysis of various mathematical symbols. It is the study of unknown quantities, which are often depicted with the help of variables in mathematics. Algebra has a plethora of formulas and identities for th 4 min read
Chapter 5: Arithmetic Progressions
- Arithmetic Progressions Class 10- NCERT Notes Arithmetic Progressions (AP) are fundamental sequences in mathematics where each term after the first is obtained by adding a constant difference to the previous term. Understanding APs is crucial for solving problems related to sequences and series in Class 10 Mathematics. These notes cover the ess 7 min read
- Sequences and Series A sequence is an ordered list of numbers following a specific rule. Each number in a sequence is called a "term." The order in which terms are arranged is crucial, as each term has a specific position, often denoted as an, where n indicates the position in the sequence. For example: 2, 5, 8, 11, 14 7 min read
- Arithmetic Progression Arithmetic progression (AP) is simply a sequence of numbers such that the difference between any two consecutive terms is constant. Real World Examples of AP Natural Numbers: 1, 2, 3, 4, 5, . . . with a common difference 1Even Numbers: 2, 4, 6, 8, 10, . . . with a common difference 2Odd Numbers: 1, 6 min read
- Arithmetic Progression - Common difference and Nth term | Class 10 Maths Arithmetic Progression is a sequence of numbers where the difference between any two successive numbers is constant. For example 1, 3, 5, 7, 9....... is in a series which has a common difference (3 - 1) between two successive terms is equal to 2. If we take natural numbers as an example of series 1, 5 min read
- How to find the nth term of an Arithmetic Sequence? Answer: Nth term of an Arithmetic Sequence, an = a1 + (N-1)d ⇢ [First term + (Last term - 1)×common difference]Arithmetic is a part of mathematics that works with different types of numbers, and fractions, applying different operations on numbers like addition, multiplication, etc. The word Arithmet 7 min read
- Arithmetic Progression | Sum of First n Terms | Class 10 Maths Arithmetic Progression is a sequence of numbers where the difference between any two successive numbers is constant. For example 1, 3, 5, 7, 9……. is in a series which has a common difference (3 – 1) between two successive terms is equal to 2. If we take natural numbers as an example of series 1, 2, 8 min read
- Arithmetic Mean Arithmetic Mean, commonly known as the average, is a fundamental measure of central tendency in statistics. It is defined as the ratio of all the values or observations to the total number of values or observations. Arithmetic Mean is one of the fundamental formulas used in mathematics and it is hig 13 min read
Chapter 6: Triangles
- Triangles in Geometry Triangles in Geometry: A Triangle is a polygon with three sides and three corners. The corners are also known as vertices, and the sides that connect them are called edges. The interior of a triangle is a two-dimensional region. A triangle is the simplest form of a Polygon. Triangles can be classifi 15+ min read
- Similar Triangles Similar Triangles are triangles with the same shape but can have variable sizes. Similar triangles have corresponding sides in proportion to each other and corresponding angles equal to each other. Similar triangles are different from congruent triangles. Two congruent figures are always similar, bu 15+ min read
- Criteria for Similarity of Triangles Things are often referred similar when the physical structure or patterns they show have similar properties, Sometimes two objects may vary in size but because of their physical similarities, they are called similar objects. For example, a bigger Square will always be similar to a smaller square. In 9 min read
- Basic Proportionality Theorem (BPT) Class 10 | Proof and Examples Basic Proportionality Theorem: Thales theorem is one of the most fundamental theorems in geometry that relates the parts of the length of sides of triangles. The other name of the Thales theorem is the Basic Proportionality Theorem or BPT. BPT states that if a line is parallel to a side of a triangl 8 min read
- Pythagoras Theorem | Formula, Proof and Examples Pythagoras Theorem explains the relationship between the three sides of a right-angled triangle and helps us find the length of a missing side if the other two sides are known. It is also known as the Pythagorean theorem. It states that in a right-angled triangle, the square of the hypotenuse is equ 10 min read
Chapter 7: Coordinate Geometry
- Coordinate Geometry Coordinate geometry is the branch of mathematics that deals with plotting the curve on the coordinate axes. Various curves can be plotted on the coordinate plane using coordinate geometry formulas. Co-ordinate geometry uses algebraic equations to plot various curves on the coordinate plane. One of t 11 min read
- Distance Formula Class 10 Maths The distance formula is one of the important concepts in coordinate geometry which is used widely. By using the distance formula we can find the shortest distance i.e drawing a straight line between points. There are two ways to find the distance between points: Pythagorean theoremDistance formulaTa 9 min read
- Distance Between Two Points Distance Between Two Points is the length of line segment that connects any two points in a coordinate plane in coordinate geometry. It can be calculated using a distance formula for 2D or 3D. It represents the shortest path between two locations in a given space. In this article, we will learn how 6 min read
- Section Formula Section Formula is a useful tool in coordinate geometry, which helps us find the coordinate of any point on a line which is dividing the line into some known ratio. Suppose a point divides a line segment into two parts which may be equal or not, with the help of the section formula we can find the c 15 min read
- How to find the ratio in which a point divides a line? Answer: To find the ratio in which a point divides a line we use the following formula [Tex]x = \frac{m_1x_2+m_2x_1}{m_1+m_2} [/Tex][Tex]y = \frac{m_1y_2+m_2y_1}{m_1+m_2}[/Tex]Geo means Earth and metry means measurement. Geometry is a branch of mathematics that deals with distance, shapes, sizes, r 4 min read
- How to find the Trisection Points of a Line? To find the trisection points of a line segment, you need to divide the segment into three equal parts. This involves finding the points that divide the segment into three equal lengths. In this article, we will answer "How to find the Trisection Points of a Line?" in detail including section formul 4 min read
- How to find the Centroid of a Triangle? Answer: The Centroid for the triangle is calculated using the formula[Tex]\left (\frac{[x1+x2+x3]}{3}, \frac{[y1+y2+y3]}{3}\right)[/Tex]A triangle consists of three sides and three interior angles. Centroid refers to the center of an object. Coming to the centroid of the triangle, is defined as the 4 min read
- Area of a Triangle in Coordinate Geometry Coordinate geometry is defined as the study of geometry using the coordinate points on the plane with any dimension. Using coordinate geometry, it is possible to find the distance between two points, divide lines in a ratio, find the mid-point of a line, calculate the area of a triangle in the Carte 8 min read
Chapter 8: Introduction to Trigonometry
- Trigonometric Ratios Trigonometric Ratios: There are three sides of a triangle Hypotenuse, Adjacent, and Opposite. The ratio between these sides based on the angle between them is called Trigonometric Ratio. The six trigonometric ratios are sine (sin), cosine (cos), tangent (tan), cotangent (cot), cosecant (cosec), and 7 min read
- Unit Circle: Definition, Formula, Diagram and Solved Examples Unit Circle is a Circle whose radius is 1. The center of unit circle is at origin(0,0) on the axis. The circumference of Unit Circle is 2π units, whereas area of Unit Circle is π units2. It carries all the properties of Circle. Unit Circle has the equation x2 + y2 = 1. This Unit Circle helps in defi 7 min read
- Trigonometric Ratios of Some Specific Angles Trigonometry is all about triangles or to be more precise the relationship between the angles and sides of a triangle (right-angled triangle). In this article, we will be discussing the ratio of sides of a right-angled triangle concerning its acute angle called trigonometric ratios of the angle and 6 min read
- Trigonometric Identities Trigonometric identities play an important role in simplifying expressions and solving equations involving trigonometric functions. These identities, which involve relationships between angles and sides of triangles, are widely used in fields like geometry, engineering, and physics. In this article, 11 min read
Chapter 9: Some Applications of Trigonometry
- Height and Distance | Applications of Trigonometry Height and Distance: Height is the measurement of an item in the vertical direction, whereas distance is the measurement of an object in the horizontal direction. Heights and Distances are the real-life applications of trigonometry which is useful to astronomers, navigators, architects, surveyors, e 9 min read
Chapter 10: Circles
- Tangent to a Circle Tangent in Circles are the line segments that touch the given curve only at one particular point. Tangent is a Greek word meaning "To Touch". For a circle, we can say that the line which touches the circle from the outside at one single point on the circumference is called the tangent of the circle. 10 min read
- Theorem - The tangent at any point of a circle is perpendicular to the radius through the point of contact - Circles | Class 10 Maths Tangent is a straight line drawn from an external point that touches a circle at exactly one point on the circumference of the circle. There can be an infinite number of tangents of a circle. These tangents follow certain properties that can be used as identities to perform mathematical computations 3 min read
- Theorem - The lengths of tangents drawn from an external point to a circle are equal - Circles | Class 10 Maths Tangent is a straight line drawn from an external point that touches a circle at exactly one point on the circumference of the circle. There can be an infinite number of tangents of a circle. These tangents follow certain properties that can be used as identities to perform mathematical computations 5 min read
- Number of Tangents from a Point on a Circle A circle is a collection of all the points in a plane that are at a constant distance from a particular point. This distance is called the radius of the circle and the fixed point is called the centre. A straight line and a circle can co-exist in three ways, one can be a straight line with no inter 12 min read
Chapter 11: Constructions
- Division of Line Segment in Given Ratio - Constructions | Class 10 Maths Line is a straight one-dimensional figure that has no thickness. In geometry, a line extends endlessly in both directions. It is described as the shortest distance between any two points. A-line can also be understood as multiple points connected to each other in one specific direction without a gap 4 min read
- Construction of Similar Triangles The basic construction techniques allow the construction of perpendicular bisectors, angle bisectors, and so on. These basic techniques can be used for more complex constructions. These constructions are very essential for the designers who design buildings, roads, machines .. Etc. So, these techniq 8 min read
- Constructions of Tangents to a Circle A line can pass through a circle in three ways- it can either pass through only a single point of the circle, intersect it, or it can pass outside it. A line passing through a single point of a circle is called a tangent. When a line intersects the circle at two points, we call that line a tangent. 8 min read
Chapter 12: Areas related to circles
- Area of a Circle: Formula, Derivation, Examples Area of a Circle is the measure of the two-dimensional space occupied by a circle. It is mostly calculated by the size of the circle's radius which is the distance from the center of the circle to any point on its edge. The area of a circle is proportional to the radius of the circle. Area of Circle 10 min read
- Circumference of Circle - Definition, Perimeter Formula, and Examples The circumference of a circle is the distance around its boundary, much like the perimeter of any other shape. It is a key concept in geometry, particularly when dealing with circles in real-world applications such as measuring the distance traveled by wheels or calculating the boundary of round obj 8 min read
- Sector of a Circle Sector of a Circle is one of the components of a circle like a segment which students learn in their academic years as it is one of the important geometric shapes. The sector of a circle is a section of a circle formed by the arc and its two radii and it is produced when a section of the circle's ci 12 min read
- Arc Length Formula Arc length is the distance along the curved path of a circle or any part of its circumference. We define arc length as measuring the length of a slice of pizza crust. Arc length is calculated using the simple formula: Arc Length= r × θ where 'r' is the radius of the circle and 'θ' is the angle in ra 8 min read
Chapter 13: Surface Areas and Volume
- Surface Area of Cuboid The surface area of a cuboid is the total space occupied by all its surfaces/sides. In geometry, a three-dimensional shape having six rectangular faces is called a cuboid. A cuboid is also known as a regular hexahedron and has six rectangular faces, eight vertices, and twelve edges with congruent, o 12 min read
- Volume of Cuboid | Formula and Examples Volume of a cuboid is calculated using the formula V = L × B × H, where V represents the volume in cubic units, L stands for length, B for breadth, and H for height. Here, the breadth and width of a cuboid are the same things. The volume signifies the amount of space occupied by the cuboid in three 8 min read
- Surface Area of Cube | Curved & Total Surface Area Surface area of a cube is defined as the total area covered by all the faces of a cube. In geometry, the cube is a fascinating three-dimensional object that we encounter daily, from dice to ice cubes. But have you ever wondered about the total area that covers a cube? This is what we call the surfac 15 min read
- Volume of a Cube Volume of a Cube is defined as the total number of cubic units occupied by the cube completely. A cube is a three-dimensional solid figure, having 6 square faces. Volume is nothing but the total space occupied by an object. An object with a larger volume would occupy more space. The volume of the cu 9 min read
- Surface Area of Cylinder | Curved and Total Surface Area of Cylinder Surface Area of a Cylinder is the amount of space covered by the flat surface of the cylinder's bases and the curved surface of the cylinder. The total surface area of the cylinder includes the area of the cylinder's two circular bases as well as the area of the curving surface. The volume of a cyli 10 min read
- Volume of a Cylinder| Formula, Definition and Examples Volume of a cylinder is a fundamental concept in geometry and plays a crucial role in various real-life applications. It is a measure which signifies the amount of material the cylinder can carry. It is also defined as the space occupied by the Cylinder. The formula for the volume of a cylinder is π 11 min read
- Surface Area of Cone Surface Area of a Cone is the total area encompassing the circular base and the curved surface of the cone. A cone has two types of surface areas. If the radius of the base is 'r' and the slant height is 'l', we use two formulas: Total Surface Area (TSA) of the cone = πr(r + l)Curved Surface Area (C 8 min read
- Volume of Cone- Formula, Derivation and Examples Volume of a cone can be defined as the space occupied by the cone. As we know, a cone is a three-dimensional geometric shape with a circular base and a single apex (vertex). Let's learn about Volume of Cone in detail, including its Formula, Examples, and the Frustum of Cone. Volume of ConeA cone's v 10 min read
- Surface Area of Sphere | Formula, Derivation and Solved Examples A sphere is a three-dimensional object with all points on its surface equidistant from its center, giving it a perfectly round shape. The surface area of a sphere is the total area that covers its outer surface. To calculate the surface area of a sphere with radius r, we use the formula: Surface Are 8 min read
- Volume of a Sphere The volume of a sphere helps us understand how much space a perfectly round object occupies, from tiny balls to large planets. Using the simple volume of sphere formula, you can easily calculate the space inside any sphere. Whether you're curious about the volume of a solid sphere in math or science 8 min read
- Surface Area of a Hemisphere A hemisphere is a 3D shape that is half of a sphere's volume and surface area. The surface area of a hemisphere comprises both the curved region and the base area combined. Hemisphere's Total Surface Area (TSA) = Curved Surface Area + Base Area = 3πr² square units.Curved Surface Area (CSA) = 2πr² sq 13 min read
- Volume of Hemisphere Volume of a shape is defined as how much capacity a shape has or we can say how much material was required to form that shape. A hemisphere, derived from the Greek words "hemi" (meaning half) and "sphere," is simply half of a sphere. If you imagine slicing a perfectly round sphere into two equal hal 6 min read
- Volume of Combination of Solids When two or more two solids are combined and the combination comes out useful, a shape that can be found in reality is called a combination of solids. When Solids are taught, the major focus is always on the point of their real-life use and applications, For example, a cylinder can be seen in Pipes 9 min read
- Frustum of Cone Frustum of a cone is a special shape that is formed when we cut the cone with a plane parallel to its base. The cone is a three-dimensional shape having a circular base and a vertex. So the frustum of a cone is a solid volume that is formed by removing a part of the cone with a plane parallel to cir 10 min read
- Conversion of solids - Surface Areas and Volumes Conversions or changes are now a normal feature of our everyday lives. A goldsmith, for instance, melts a strip of gold to turn it into a gem. Likewise, a kid plays with clay forms it into various toys, a carpenter uses the wooden logs to shape various items/furniture for housekeeping. Likewise, for 4 min read
- Surface Areas and Volumes Surface Area and Volume are two fundamental properties of a three-dimensional (3D) shape that help us understand and measure the space they occupy and their outer surfaces. Knowing how to determine surface area and volumes can be incredibly practical and handy in cases where you want to calculate th 10 min read
Chapter 14: Statistics
- How to find Mean of grouped data by direct method? Statistics involves gathering, organizing, analyzing, interpreting, and presenting data to form opinions and make decisions. Applications range from educators computing average student scores and government officials conducting censuses to demographic analysis. Understanding and utilizing statistica 9 min read
- Shortcut Method for Arithmetic Mean Statistics, in layman's words, is the process of gathering, classifying, examining, interpreting, and finally presenting information in an understandable manner so that one can form an opinion and, if necessary, take action. Examples: A teacher collects students' grades, organizes them in ascending 6 min read
- How to Calculate Mean using Step Deviation Method? Step Deviation Method is a simplified way to calculate the mean of a grouped frequency distribution, especially when the class intervals are uniform. In simple words, statistics implies the process of gathering, sorting, examining, interpreting and then understandably presenting the data to enable o 7 min read
- Graphical determination of Median A measure of central tendency that determines the centrally located value of a given series is known as the Median. The number of values of the series below and above the given series is always equal. To determine the median value of a given series, it is first managed in increasing or decreasing or 5 min read
- Ogive (Cumulative Frequency Curve) and its Types A method of presenting data in the form of graphs that provides a quick and easier way to understand the trends of the given set of data is known as Graphic Presentation. The two types of graphs through which a given set of data can be presented are Frequency Distribution Graphs and Time Series Grap 6 min read
Chapter 15: Probability
- Types of Events in Probability Whenever an experiment is performed whose outcomes cannot be predicted with certainty, it is called a random experiment. In such cases, we can only measure which of the events is more likely or less likely to happen. This likelihood of events is measured in terms of probability and events refer to t 13 min read
- Dependent and Independent Events Dependent and Independent Events are the types of events that occur in probability. Suppose we have two events say Event A and Event B then if Event A and Event B are dependent events then the occurrence of one event is dependent on the occurrence of other events if they are independent events then 8 min read
- Experimental Probability Experimental probability, also known as empirical probability, is a concept in mathematics that deals with estimating the likelihood of an event occurring based on actual experimental results. Unlike theoretical probability, which predicts outcomes based on known possibilities, experimental probabil 8 min read
- Probability Theory Probability theory is a branch of mathematics that deals with quantifying the likelihood of events occurring. It provides tools to analyze situations involving uncertainty and helps in determining how likely certain outcomes are. According to Probability Theory Probability is defined as the chance o 10 min read
- CBSE Class 10th Maths Formulas: Chapter Wise Formula and Points Mathematics is one of the most scoring subject in CBSE Class 10th board exam. So Students are advised to prepare well for Math in order to score good marks in CBSE Class 10 board exam. GeeksforGeeks has curated the chapter wise Math formulae for CBSE Class 10th exam. These Formulae include chapters 15+ min read
- NCERT Solutions for Class 10 Maths 2024-25: Chapter Wise PDF Download NCERT Solutions for Class 10 Maths are tailored by subject matter experts to assist 10 students in securing top marks in their 10 board exams. As we know mathematics is the highest-scoring subject in the CBSE Class 10th board exam This complete resource includes all questions and answers from the CB 15+ min read
- RD Sharma Class 10 Solutions RD Sharma Class 10 Solutions offer excellent reference material for students, enabling them to develop a firm understanding of the concepts covered. in each chapter of the textbook. As Class 10 mathematics is categorized into various crucial topics such as Algebra, Geometry, and Trigonometry, which 9 min read
- Mathematics
- School Learning
- Technical Scripter
- Maths-Class-9
- Probability
- Technical Scripter 2020
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
This topic is relevant for:

Experimental Probability
Here we will learn about experimental probability, including using the relative frequency and finding the probability distribution.
There are also probability distribution worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is experimental probability?
Experimental probability i s the probability of an event happening based on an experiment or observation.
To calculate the experimental probability of an event, we calculate the relative frequency of the event.
We can also express this as R=\frac{f}{n} where R is the relative frequency, f is the frequency of the event occurring, and n is the number of trials of the experiment.
If we find the relative frequency for all possible events from the experiment we can write the probability distribution for that experiment.
The relative frequency, experimental probability and empirical probability are the same thing and are calculated using the data from random experiments. They also have a key use in real-life problem solving.
For example, Jo made a four-sided spinner out of cardboard and a pencil.

She spun the spinner 50 times. The table shows the number of times the spinner landed on each of the numbers 1 to 4. The final column shows the relative frequency.
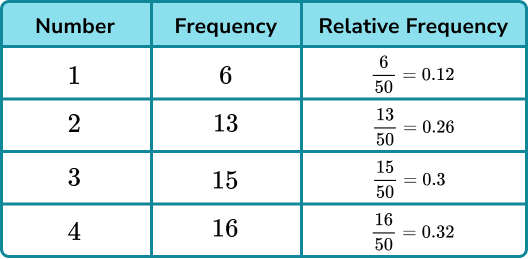
The relative frequencies of all possible events will add up to 1.
This is because the events are mutually exclusive.
Step-by-step guide: Mutually exclusive events

Experimental probability vs theoretical probability
You can see that the relative frequencies are not equal to the theoretical probabilities we would expect if the spinner was fair.
If the spinner is fair, the more times an experiment is done the closer the relative frequencies should be to the theoretical probabilities.
In this case the theoretical probability of each section of the spinner would be 0.25, or \frac{1}{4}.
Step-by-step guide: Theoretical probability
How to find an experimental probability distribution
In order to calculate an experimental probability distribution:
Draw a table showing the frequency of each outcome in the experiment.
Determine the total number of trials.
Write the experimental probability (relative frequency) of the required outcome(s).

Explain how to find an experimental probability distribution

Experimental probability worksheet
Get your free experimental probability worksheet of 20+ questions and answers. Includes reasoning and applied questions.
Related lessons on probability distribution
Experimental probability is part of our series of lessons to support revision on probability distribution . You may find it helpful to start with the main probability distribution lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
- Probability distribution
- Relative frequency
- Expected frequency
Experimental probability examples
Example 1: finding an experimental probability distribution.
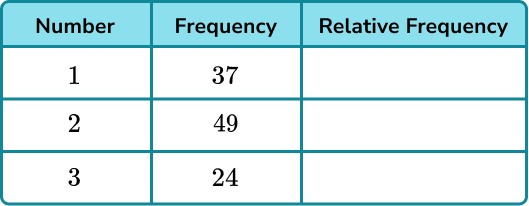
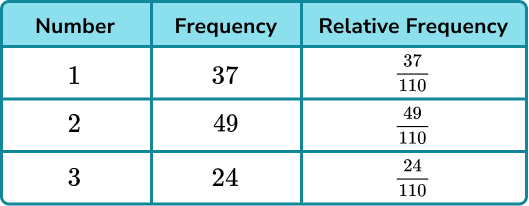
A 3 sided spinner numbered 1,2, and 3 is spun and the results recorded.

Find the probability distribution for the 3 sided spinner from these experimental results.
A table of results has already been provided. We can add an extra column for the relative frequencies.
2 Determine the total number of trials
3 Write the experimental probability (relative frequency) of the required outcome(s).
Divide each frequency by 110 to find the relative frequencies.
Example 2: finding an experimental probability distribution
A normal 6 sided die is rolled 50 times. A tally chart was used to record the results.
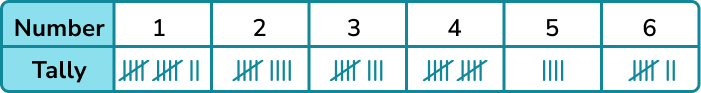
Determine the probability distribution for the 6 sided die. Give your answers as decimals.
Use the tally chart to find the frequencies and add a row for the relative frequencies.
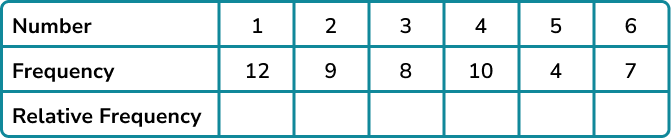
The question stated that the experiment had 50 trials. We can also check that the frequencies add to 50.
Divide each frequency by 50 to find the relative frequencies.
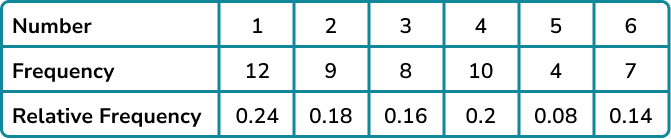
Example 3: using an experimental probability distribution
A student made a biased die and wanted to find its probability distribution for use in a game. They rolled the die 100 times and recorded the results.
By calculating the probability distribution for the die, determine the probability of the die landing on a 3 or a 4.
The die was rolled 100 times.
We can find the probability of rolling a 3 or a 4 by adding the relative frequencies for those numbers.
P(3 or 4) = 0.22 + 0.25 = 0.47
Example 4: calculating the relative frequency without a known frequency of outcomes
A research study asked 1200 people how they commute to work. 640 travelled by car, 174 used the bus, and the rest walked. Determine the relative frequency of someone not commuting to work by car.
Writing the known information into a table, we have
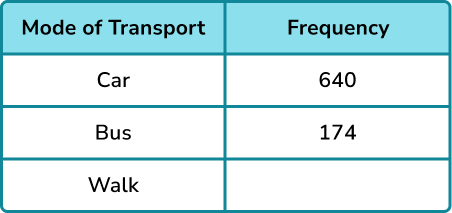
We currently do not know the frequency of people who walked to work. We can calculate this as we know the total frequency.
The number of people who walked to work is equal to
1200-(640+174)=386.
We now have the full table,
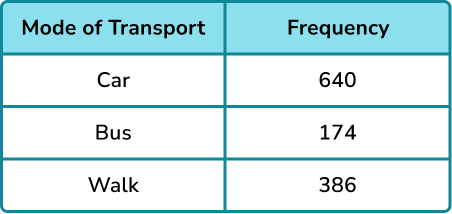
The total frequency is 1200.
Divide each frequency by the total number of people (1200), we have
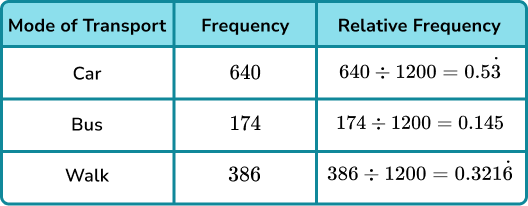
The relative frequency of someone walking to work is 0.321\dot{6} .
How to find a frequency using an experimental probability
In order to calculate a frequency using an experimental probability:
Multiply the total frequency by the experimental probability.
Explain how to find a frequency using an experimental probability

Example 5: calculating a frequency
A dice was rolled 300 times. The experimental probability of rolling an even number is \frac{27}{50}. How many times was an even number rolled?
An even number was rolled 162 times.
Example 6: calculating a frequency
A bag contains different coloured counters. A counter is selected at random and replaced back into the bag 240 times. The probability distribution of the experiment is given below.

Determine the number of times a blue counter was selected.
As the events are mutually exclusive, the sum of the probabilities must be equal to 1. This means that we can determine the value of x.
1-(0.4+0.25+0.15)=0.2
The experimental probability (relative frequency) of a blue counter is 0.2.
Multiplying the total frequency by 0.1, we have
240 \times 0.2=48.
A blue counter was selected 48 times.
Common misconceptions
- Forgetting the differences between theoretical and experimental probability
It is common to forget to use the relative frequencies from experiments for probability questions and use the theoretical probabilities instead. For example, they may be asked to find the probability of a die landing on an even number based on an experiment and the student will incorrectly answer it as 0.5.
- The relative frequency is not an integer
The relative frequency is the same as the experimental probability. This value is written as a fraction, decimal or percentage, not an integer.
Practice experimental probability questions
1. A coin is flipped 80 times and the results recorded.

Determine the probability distribution of the coin.

As the number of tosses is 80, dividing the frequencies for the number of heads and the number of tails by 80, we have
2. A 6 sided die is rolled 160 times and the results recorded.
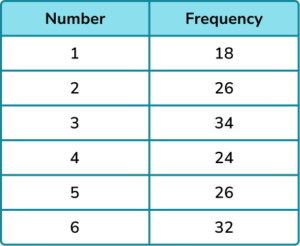
Determine the probability distribution of the die. Write your answers as fractions in their simplest form.
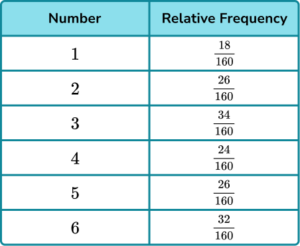
Dividing the frequencies of each number by 160, we get
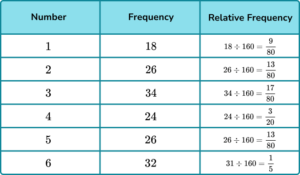
3. A 3 -sided spinner is spun and the results recorded.
Find the probability distribution of the spinner, giving you answers as decimals to 2 decimal places.
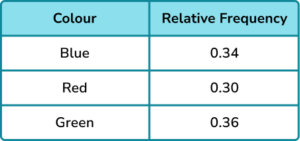
Dividing the frequencies of each colour by 128 and simplifying, we have

4. A 3 -sided spinner is spun and the results recorded.
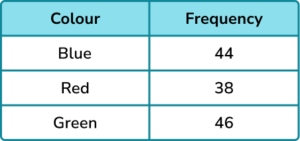
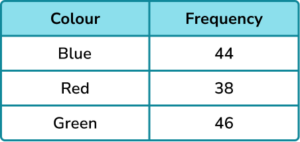
Find the probability of the spinner not landing on red. Give your answer as a fraction.
Add the frequencies of blue and green and divide by 128.
5. A card is picked at random from a deck and then replaced. This was repeated 4000 times. The probability distribution of the experiment is given below.

How many times was a club picked?

6. Find the missing frequency from the probability distribution.
The total frequency is calculated by dividing the frequency by the relative frequency.
Experimental probability GCSE questions
1. A 4 sided spinner was spun in an experiment and the results recorded.
(a) Complete the relative frequency column. Give your answers as decimals.
(b) Find the probability of the spinner landing on a square number.
Total frequency of 80.
2 relative frequencies correct.
All 4 relative frequencies correct 0.225, \ 0.2, \ 0.3375, \ 0.2375.
Relative frequencies of 1 and 4 used.
0.4625 or equivalent
2. A 3 sided spinner was spun and the results recorded.
Complete the table.
Process to find total frequency or use of ratio with 36 and 0.3.
3. Ben flipped a coin 20 times and recorded the results.

(a) Ben says, “the coin must be biased because I got a lot more heads than tails”.
Comment on Ben’s statement.
(b) Fred takes the same coin and flips it another 80 times and records the results.

Use the information to find a probability distribution for the coin.

Stating that Ben’s statement may be false.
Mentioning that 20 times is not enough trials.
Evidence of use of both sets of results from Ben and Fred.
Process of dividing by 100.
P(heads) = 0.48 or equivalent
P(tails) = 0.52 or equivalent
Learning checklist
You have now learned how to:
- Use a probability model to predict the outcomes of future experiments; understand that empirical unbiased samples tend towards theoretical probability distributions, with increasing sample size
The next lessons are
- How to calculate probability
- Combined events probability
- Describing probability
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.
Privacy Overview
- The Basic math blog
- Member Login
- Pre-Algebra Lessons
- Pre-Algebra Word Problems
- Pre-Algebra Calculators
- Algebra Lessons
- Algebra Word Problems
- Algebra Proofs
- Advanced Algebra
- Algebra Calculators
- Geometry Lessons
- Geometry Word Problems
- Geometry Proofs
- Geometry Calculators
- Trigonometry Lessons
- Numeration System
- Basic Concepts of Set Theory
- Consumer Math
- Baseball Math
- Math for Nurses
- Statistics Made Easy
- High School Physics
- Basic Mathematics Store
- Math Vocabulary Quizzes
- SAT Math Prep
- Math Skills by Grade Level
- Ask an Expert
- Other Websites
- K-12 Worksheets
- Worksheets Generator
- Algebra Worksheets
- Geometry Worksheets
- Fun Online Math Games
- Pre-Algebra Games
- Math Puzzles
- Math Tricks
Experimental probability
Experimental probability (EP), also called empirical probability or relative frequency , is probability based on data collected from repeated trials.
Experimental probability formula
Let n represent the total number of trials or the number of times an experiment is done. Let p represent the number of times an event occurred while performing this experiment n times.
Example #1: A manufacturer makes 50,000 cell phones every month. After inspecting 1000 phones, the manufacturer found that 20 phones are defective. What is the probability that you will buy a phone that is defective? Predict how many phones will be defective next month.
The total number of times the experiment is conducted is n = 1000
The number of times an event occurred is p = 20
Experimental probability is performed when authorities want to know how the public feels about a matter. Since it is not possible to ask every single person in the country, they may conduct a survey by asking a sample of the entire population. This is called population sampling. Example #2 is an example of this situation.
There are about 319 million people living in the USA. Pretend that a survey of 1 million people revealed that 300,000 people think that all cars should be electric. What is the probability that someone chosen randomly does not like electric car? How many people like electric cars?
Notice that the number of people who do not like electric cars is 1000000 - 300000 = 700000
Difference between experimental probability and theoretical probability

You can argue the same thing using a die, a coin, and a spinner. We will though use a coin and a spinner to help you see the difference.
Using a coin
In theoretical probability, we say that "each outcome is equally likely " without the actual experiment. For instance, without flipping a coin, you know that the outcome could either be heads or tails. If the coin is not altered, we argue that each outcome (heads or tails) is equally likely. In other words, we are saying that in theory or (supposition, conjecture, speculation, assumption, educated guess) the probability to get heads is 50% or the probability to get tails in 50%. Since you did not actually flip the coin, you are making an assumption based on logic.
The logic is that there are 2 possible outcomes and since you are choosing 1 of the 2 outcomes, the probability is 1/2 or 50%. This is theoretical probability or guessing probability or probability based on assumption.
In the example above about flipping a coin, suppose you are looking for the probability to get a head.
Then, the number of favorable outcomes is 1 and the number of possible outcomes is 2.
In experimental probability, we want to take the guess work out of the picture, by doing the experiment to see how many times heads or teals will come up. If you flip a coin 1000 times, you might realize that it landed on heads only 400 times. In this case, the probability to get heads is only 40%.
Your experiment may not even show tails until after the 4th flip and yet in the end you ended up with more tails than heads.
If you repeat the experiment another day, you may find a completely different result. May be this time the number of heads is 600 and the number of tails is 400.
Using a spinner
Suppose a spinner has four equal-sized sections that are red, green, black, and yellow.
In theoretical probability, you will not spin the spinner. Instead, you will say that the probability to get green is one-fourth or 25%. Why 25%? The total number of outcomes is 4 and the number of favorable outcomes is 1.
1/4 = 0.25 = 25%
However, in experimental probability, you may decide to spin the spinner 50 times or even more to see how many times you will get each color.
Suppose you spin the spinner 50 times. It is quite possible that you may end up with the result shown below:
Red: 10 Green: 15 Black: 5 Yellow: 20
Now, the probability to get green is 15/50 = 0.3 = 30%
As you can see, experimental probability is based more on facts, data collected, experiment or research!
Theoretical probability
Special Math Topics
Applied math.
About me :: Privacy policy :: Disclaimer :: Donate Careers in mathematics
Copyright © 2008-2021. Basic-mathematics.com. All right reserved
- Math tutors
- Math classes
- 1st Grade Math Worksheets
- 2nd Grade Math Worksheets
- 3rd Grade Math Worksheets
- 4th Grade Math Worksheets
- 5th Grade Math Worksheets
- 6th Grade Math Worksheets
- 7th Grade Math Worksheets
- 8th Grade Math Worksheets
- Knowledge Base
Experimental Probability – Definition with Examples
Updated on January 9, 2024
At Brighterly , we believe that a solid understanding of mathematics can empower our children to do great things. That’s why we’re committed to making complex math concepts accessible, engaging, and fun for all children. Among the myriad of mathematical topics we cover, one of the more practical, yet fascinating, is experimental probability.
Experimental probability is like the bridge between math and the real world, offering a hands-on approach to understanding likelihood and chance. It’s all about observation, data collection, and making sense of the patterns that emerge. Experimental probability takes us beyond the theoretical and into the empirical, providing our children with a richer, fuller understanding of how probability works.
What Is Experimental Probability?
Experimental probability is a concept that children often encounter in their mathematical journey, and it provides a fantastic way to understand how probability works in the real world. It is a type of probability that we calculate based on the outcomes of an experiment or activity, as opposed to theoretical probability which we calculate using mathematical principles. It’s all about doing rather than just thinking.
Imagine you’re flipping a coin. The theoretical probability of getting a heads or tails is 50%, or 0.5, because these are the only two possible outcomes. However, if you flip the coin 10 times and get 7 heads and 3 tails, the experimental probability of getting heads is 70% (or 0.7), and for tails, it’s 30% (or 0.3). This is because experimental probability depends on the actual results of the experiment.
Definition of Experimental Probability
The definition of experimental probability is the ratio of the number of times an event occurs to the total number of trials or times the activity is performed. It is calculated after conducting an experiment or activity, and can often differ from theoretical probability because of the variability and unpredictability of real-world events.
Calculating Experimental Probability
The process of calculating experimental probability involves two steps: conducting the experiment to gather data, and then using that data to calculate the probability. The formula for calculating experimental probability is:
P(E) = Number of times event E occurs / Total number of trials
For example, if you roll a dice 60 times, and the number 4 comes up 15 times, the experimental probability of rolling a 4 is calculated as 15 (the number of times 4 occurs) divided by 60 (the total number of trials), which equals 0.25, or 25%.
Examples of Experimental Probability
To better understand this concept, let’s explore some real-world examples of experimental probability:
In a bag of 30 marbles, 10 are blue, 10 are green, and 10 are red. If you randomly pick a marble 30 times, replacing the marble each time, and you get 12 blue, 8 green, and 10 red marbles, the experimental probability for each color would be calculated as follows:
- Blue: 12/30 = 0.4 or 40%
- Green: 8/30 = 0.267 or 26.7%
- Red: 10/30 = 0.333 or 33.3%
In a deck of 52 playing cards, if you draw a card 52 times, replacing the card each time, and you draw a heart 15 times, the experimental probability of drawing a heart is 15/52 = 0.288 or 28.8%.
Properties of Experimental Probability
Experimental probability, as with any type of probability, possesses some key properties. It will always be a value between 0 and 1 (or 0% and 100% when expressed as a percentage). This makes sense, as it’s impossible for an event to occur less than 0 times (probability = 0), or more times than the total number of trials (probability = 1).
Another key property is that the sum of the probabilities of all possible outcomes will equal 1. For example, in our earlier coin flipping example, the sum of the experimental probabilities for getting heads (0.7) and tails (0.3) equals 1.
Key Factors Affecting Experimental Probability
The key factor affecting experimental probability is the number of trials. In general, the more trials are performed, the closer the experimental probability gets to the theoretical probability. This principle is known as the Law of Large Numbers.
Other factors that can affect experimental probability include inaccuracies in data collection and environmental variables, such as the fairness of a coin or die, the method of drawing cards, and so on.
Difference Between Experimental and Theoretical Probability
The main difference between experimental and theoretical probability lies in their calculation methods. Theoretical probability is determined mathematically, using the known outcomes of an event, while experimental probability is determined empirically, using data from actual trials of the event.
In theory, a coin has a 50% chance of landing on heads, but in an experiment, it might not. Over the long run, the experimental probability will likely get closer to the theoretical probability, thanks to the Law of Large Numbers.
Formulas for Calculating Experimental Probability
As mentioned earlier, the formula for calculating experimental probability is straightforward:
Here, ‘P(E)’ represents the probability of event E occurring.
Writing Formulas for Experimental Probability
Let’s get into the details of how to write formulas for experimental probability. For any given event E, you can express the experimental probability of that event occurring as a fraction, decimal, or percentage using the aforementioned formula. Just remember to divide the number of times the event occurred by the total number of trials.
For example, if you’re trying to find the experimental probability of drawing a heart from a deck of cards and you drew a heart 13 times out of 52 trials, you’d write it as follows:
P(Heart) = 13/52 ≈ 0.25 = 25%
Use Cases of Experimental Probability in Real Life
Experimental probability finds its use in various real-life scenarios, from games and sports to weather forecasting and medical research. For example, predicting the outcome of a football game based on past performances is a use of experimental probability. Likewise, weather forecasts use data from previous years to predict the likelihood of certain weather conditions. Experimental probability is also used in clinical trials to determine the effectiveness of a new drug or treatment.
Practice Problems on Experimental Probability
To fully understand experimental probability, it’s helpful to solve some practice problems. Try the following scenarios:
- You toss a coin 50 times and get heads 29 times. What is the experimental probability of getting heads?
- You draw a card from a deck of 52 cards 100 times and draw a queen 22 times. What is the experimental probability of drawing a queen?
- You roll a die 200 times and roll a 5, 40 times. What is the experimental probability of rolling a 5?
In conclusion, experimental probability offers a practical and exciting way for children to understand the concept of probability and chance. Through experiments and observations, children can learn not just how to calculate the likelihood of an event, but also develop an intuitive understanding of probability.
At Brighterly, we encourage our young learners to immerse themselves in the world of experimental probability and explore its numerous applications in real-life situations. From games and sports to weather forecasting and medical research, experimental probability has vast real-world significance. Remember, with more trials, the experimental probability tends to converge with the theoretical probability, making it a valuable tool in understanding uncertainty and making predictions.
Frequently Asked Questions on Experimental Probability
What is the formula for experimental probability.
The formula for experimental probability is: P(E) = Number of times event E occurs / Total number of trials. Here, P(E) stands for the probability of event E, which could be any event you’re examining. This formula is straightforward to use, and it allows you to compute the experimental probability accurately using your collected data.
How is experimental probability calculated?
Experimental probability is calculated by carrying out an experiment and recording the outcomes. The number of times a particular event occurs is then divided by the total number of trials conducted. For example, if you roll a dice 100 times and the number 4 comes up 20 times, the experimental probability of rolling a 4 would be 20/100 = 0.20, or 20%.
What is the difference between experimental and theoretical probability?
Theoretical probability and experimental probability differ in the ways they are determined. Theoretical probability is derived using mathematical principles, considering all possible outcomes of an event. For instance, when flipping a fair coin, the theoretical probability of getting a head is 50% since there are two equally likely outcomes – heads and tails. On the other hand, experimental probability is calculated based on actual experiments or trials. If you flip the same coin 100 times and get heads 60 times, the experimental probability of getting heads would be 60/100 = 0.60, or 60%. Over time, with a large number of trials, the experimental probability will tend to get closer to the theoretical probability. This is a consequence of the Law of Large Numbers.
- Britannica: Law of Large Numbers
- Coursera: Understanding Experimental Probability
- Wolfram MathWorld: Experimental Probability

As a seasoned educator with a Bachelor’s in Secondary Education and over three years of experience, I specialize in making mathematics accessible to students of all backgrounds through Brighterly. My expertise extends beyond teaching; I blog about innovative educational strategies and have a keen interest in child psychology and curriculum development. My approach is shaped by a belief in practical, real-life application of math, making learning both impactful and enjoyable.
Online Winter Math Camp for Grades 1-8
Join us to help your kid achieve their full math potential.

Choose kid's grade
Online Winter Math Camp for Grades 1-8 Join our Math Winter Camp and boost your child's math skills with our best tutors.
Online Winter Math Camp (1st – 8th Grades)
Online winter math camp for kids & teens.

Winter break is the perfect time to
Related math, 9500 in words.
The number 9500 is spelled as “nine thousand five hundred”. It is five hundred more than nine thousand. For example, if you have nine thousand five hundred coins, you have nine thousand coins and then five hundred extra coins, making nine thousand five hundred. Thousands Hundreds Tens Ones 9 5 0 0 How to Write […]
450 in Words
We write the number 450 as “four hundred and fifty” in words. It is four hundred plus fifty. When you have 450 marbles, it means you have four hundred marbles and fifty extra marbles. Hundreds Tens Ones 4 5 0 How to Write 450 in Words? The number 450 is written as ‘Four Hundred and […]
2600 in Words
The number 2600 is expressed in words as “two thousand six hundred”. It comes after two thousand five hundred ninety-nine. For example, if there are two thousand six hundred apples, you have two thousand five hundred ninety-nine apples and then one more. Thousands Hundreds Tens Ones 2 6 0 0 How to Write 2600 in […]
Want your kid to excel in math?
Kid’s grade

Close a child’s math gaps with a tutor!
We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

Home / United States / Math Classes / 7th Grade Math / Experimental Probability
Experimental Probability
The outcome of an actual experiment involving numerous trials is called experimental probability. Learn more about exper imental probability and its properties in this article. ...Read More Read Less
About Experimental Probability

Defining Probability
How precisely do we define experimental probability, formulation.
- Solved Examples
- Frequently Asked Questions
The mathematics of chance is known as probability (p). The probability of occurrence of an event (E) is revealed by probability.
The probability of an event can be expressed as a number between 0 and 1.
The likelihood of an impossibility is zero. A probability between 0 and 1 can be attributed to any other events that fall in between these two extremes. Experimental probability is the probability that is established based on the outcomes of an experiment. The term ‘ empirical probability ’ is also used for the same concept.
A probability that has been established by a series of tests is called an experimental probability. To ascertain their possibility, a random experiment is conducted and iterated over a number of times; each iteration is referred to as a trial .
The goal of the experiment is to determine the likelihood of an event occurring or not.
It could involve spinning a spinner, tossing a coin, or using a dice. The probability of an event is defined mathematically as the number of occurrences of the event divided by the total number of trials.
The number of times an event occurred during the experiment divided by all the times the experiment was run is known as the experimental probability of that event. Each potential result is unknown, and the collection of all potential results is referred to as the sample space .
Experimental probability is calculated using the following formula:
\(P(E)=\frac{Number~of~times~an~event~occurred~during~an~experiment}{The~total~number~of~times~the~experiment~was~conducte}\)
\(P(E)=\frac{n(E)}{n(S)}\)
n(E) = Number of events occurred
n(S) = Number of sample space
Solved Experimental Probability Examples
Example 1: The owner of a cake store is curious about the percentage of sales of his new gluten-free cupcake line. He counts the number of cakes that were sold on one day of the week, Monday, where he sold 30 regular and 70 gluten free cakes. Calculate the probability in this case.

According to the details in the question, the number of gluten free cakes is n(E) = 70 cakes.
Total number of cakes n(S) = 30 + 70 = 100 cakes.
Substituting these values in the formula.
\(P(E)=\frac{n(E)}{n(S)}\) = \(\frac{70}{100}\) = 0.7 = 70%
Hence, the owner of the cake store finds that the gluten-free cupcakes will probably make up 70% of his weekly sales.
Example 2: A baseball manager is interested to know the probability that a prospective new player will hit a home run in the game’s first at-bat. The player has 11 home runs in 1921 games throughout his career. Calculate the probability of the player hitting a home run.
The data provided is, the player has hit 11 home runs, n(E) = 11
Total number of games, n(s) = 1921 games.
\(P(E)=\frac{n(E)}{n(S)}\) = \(\frac{11}{1921}\) = 0.005726 = 0.5726%
He will therefore have a 0.5726 percent chance of hitting a home run in his first at-bat.
Example 3: A vegetable gardener is checking the likelihood that a fresh bitter gourd seed would germinate. He plants 100 seeds, and 57 of them sprout new plants. Calculate the probability in this scenario.

According to the question, the number of bitter gourd plants that sprouted is n(E) = 57.
Total number of seeds sown, n(S) = 100 seeds.
\(P(E)=\frac{n(E)}{n(S)}\) = \(\frac{57}{100}\) = 0.57 = 57%
Hence, the probability that a new bitter gourd seed will be sprout is 57% .
Example 4: Joe’s Bagel Shop sold 26 bagels in one day, 9 of which were raisin bagels. Calculate the percentage of raisin bagels that will be sold the following day using experimental probability.

As stated in the question, the number of raisin bagels, n(E) = 9.
Total number of bagels Joe sold, n(s) = 26 .
\(P(E)=\frac{n(E)}{n(S)}\) = \(\frac{9}{26}\) = 0.346 = 34.6%
As a result, there is a 34.6 percent chance that Joe will sell raisin bagels the following day.
Do you simplify the probabilities of experiments?
Yes, the ratio obtained is simplified after the ratio between the frequency of the occurrence and the total number of trials is determined.
Which type of probability — theoretical or experimental — is more accurate?
Compared to experimental probability, theoretical probability is more precise. Only if there are more trials, then the results of experimental probability will be close to the results from theoretical probability.
How can experimental probability be calculated?
Actual tests and recordings of events serve as the foundation for calculating the experimental probability of an event. It is determined by dividing the total number of trials by the number of times an event occurred.
What is the chance of getting a 1 when you throw a dice?
A ‘1’ has a 1/6 experimental probability of rolling. Six faces, numbered from 1 to 6, make up a dice. Any number between 1 and 6 can be obtained by rolling the dice, and the likelihood of getting a 1 is equal to the ratio of favorable results to all other potential outcomes, or 1/6.
Check out our other courses
Grades 1 - 12
Level 1 - 10

IMAGES
VIDEO
COMMENTS
Experimental probability is a probability that is determined on the basis of a series of experiments. A random experiment is done and is repeated many times to determine their likelihood and each repetition is known as a trial. The experiment is conducted to find the chance of an event to occur or not to occur.
Example 3: using an experimental probability distribution. A student made a biased die and wanted to find its probability distribution for use in a game. ... Emphasize that in mathematics, experimental probability is based on actual trials or experiments, as opposed to theoretical probability which is based on possible outcomes. ...
In mathematics, probability refers to the chance of occurrence of a specific event. Probability can be measured on a scale from 0 to 1. ... Let's take a look at some of the examples of experimental probability. Example 1: Ben tried to toss a ping-pong ball in a cup using 10 trials, out of which he succeeded 4 times. P(win) $= \frac{Number of ...
To find the experimental probability of an event, divide the number of observed outcomes favorable to the event by the total number of trials of the experiment. Let's go through some examples. Example 1: There are 20 students in a class.
Experimental probability, also known as empirical probability, is a concept in mathematics that deals with estimating the likelihood of an event occurring based on actual experimental results.Unlike theoretical probability, which predicts outcomes based on known possibilities, experimental probability is derived from real-life experiments and observations.
What is Probability? Probability, a branch of Math that deals with the likelihood of the occurrences of the given event. The probability values for the given experiment is usually defined between the range of numbers. The values lie between the numbers 0 and 1. ... Experimental Probability Example. Example: ...
Related lessons on probability distribution. Experimental probability is part of our series of lessons to support revision on probability distribution. You may find it helpful to start with the main probability distribution lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics.
Experimental probability is performed when authorities want to know how the public feels about a matter. Since it is not possible to ask every single person in the country, they may conduct a survey by asking a sample of the entire population. This is called population sampling. Example #2 is an example of this situation. Example #2
Experimental probability is like the bridge between math and the real world, offering a hands-on approach to understanding likelihood and chance. It's all about observation, data collection, and making sense of the patterns that emerge. Experimental probability takes us beyond the theoretical and into the empirical, providing our children ...
The mathematics of chance is known as probability (p). The probability of occurrence of an event (E) is revealed by probability. ... Each potential result is unknown, and the collection of all potential results is referred to as the sample space. Experimental probability is calculated using the following formula: ...